Eliminasi Gauss Pada Aplikasi Konduksi Pada Batang 1 Dimensi

Komputasi teknik merupakan suatu metode numerik untuk menyelesaikan persamaan matematika. Berbagai fenomena alam yang terjadi di sekitar kita tanpa disadari ternyata mampu dituliskan ke dalam persamaan matematika. Konduksi adalah salah satu fenomena alam yang sering terjadi di sekitar kita.

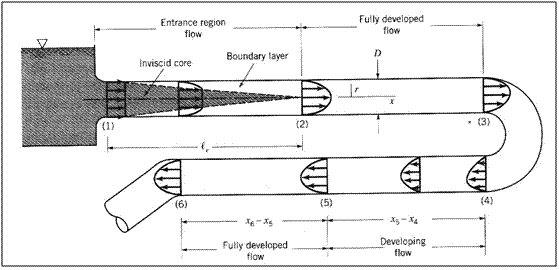
Konduksi adalah suatu fenomena perpindahan panas pada benda padat. Apabila pada suatu ujung batang kita panaskan sehingga memiliki temperatur yang lebih tinggi dari ujung batang yang lainnya, maka secara alamiah panas akan berpindah dari temperatur tinggi menuju temperatur yang lebih rendah.

Ternyata fenomena konduksi tersebut mampu diselesaikan menggunakan metode numerik sehingga kita mampu mengetahui distribusi temperatur di sepanjang batang. Berikut adalah contoh permasalahan yang ingin kita selesaikan

Pada batang terjadi perbedaan temperatur di mana pada titik B, Tb = 500 oC dan pada ujung batang A, Ta = 100 oC. Panjang batang adalah 0.5 m.

Komputasi teknik hanya dapat dilakukan jika persamaan aljabar telah diketahui, dari persoalan di atas diketahui ada 5 persamaan aljabar sebagai berikut :

300 T1 = 100 T2 + 200 Ta
200 T2 = 100 T1 + 100 T3
200 T3 = 100 T2 + 100 T4
200 T4 = 100 T3 + 100 T5
300 T5 = 100 T4 + 200 Tb

Dimana apabila kita atur, maka persamaan-persamaan di atas juga dapat ditulis sebagai berikut :

300 T1 + (-100) T2 + 0 T3 + 0 T4 + 0 T5                             = 200 Ta
(-100) T1 + 200 T2 + (-100) T3 + 0 T4 + 0 T5                      = 0
0 T1 + (-100) T2 + 200 T3 + (-100) T4 + 0 T5                      = 0
0 T1 + 0 T2 + (-100) T3 + 200 T4 + (-100) T5                      = 0
0 T1 + 0 T2 + 0 T3 + (-100) T4 + 300 T5                             = 200 Tb

Dengan metode eliminasi gauss, maka berikut langkah-langkah untuk mencari distribusi temperatur di sepanjang batang :

1. Buat pivot u sebagai faktor pengali sehingga eliminasi dapat dilakukan
2. Eliminasi dilakukan sampai baris paling bawah hanya tersisa 2 angka yang bukan nol, yaitu koefisien di depan T5 dan angka di ruas kanan.
3. Lakukan substitusi balik sehingga nilai T5, T4, T3, T2, dan T1 dapat diselesaikan

Untuk langkah-langkah di visual basic, berikut langkah-langkahnya :

1. Buat userform seperti di bawah ini

2. Buatlah program pada commandbutton sebagai berikut :

Private Sub CommandButton1_Click()

'Menyelesaikan aplikasi CFD menggunakan Eliminasi Gauss
'Arandityo Narutomo 1106107782
'Komputasi Teknik

Dim a11, a12, a13, a14, a15, a16, a21, a22, a23, a24, a25, a26 As Double
Dim a31, a32, a33, a34, a35, a36, a41, a42, a43, a44, a45, a46 As Double
Dim a51, a52, a53, a54, a55, a56, Ta, Tb As Double
Dim u1, u2, u3, u4, u5, u6, u7, u8, u9, u10 As Double
Dim b21, b22, b23, b24, b25, b26, c31, c32, c33, c34, c35, c36 As Double
Dim d41, d42, d43, d44, d45, d46, e51, e52, e53, e54, e55, e56 As Double
Dim f31, f32, f33, f34, f35, f36, g41, g42, g43, g44, g45, g46 As Double
Dim h51, h52, h53, h54, h55, h56, i41, i42, i43, i44, i45, i46 As Double
Dim j51, j52, j53, j54, j55, j56, k51, k52, k53, k54, k55, k56 As Double
Dim T1, T2, T3, T4, T5 As Double


'Mendefinisikan variable

a11 = araa11.Text
a12 = araa12.Text
a13 = araa13.Text
a14 = araa14.Text
a15 = araa15.Text

a21 = arab21.Text
a22 = arab22.Text
a23 = arab23.Text
a24 = arab24.Text
a25 = arab25.Text
a26 = arab26.Text

a31 = arac31.Text
a32 = arac32.Text
a33 = arac33.Text
a34 = arac34.Text
a35 = arac35.Text
a36 = arac36.Text

a41 = arad41.Text
a42 = arad42.Text
a43 = arad43.Text
a44 = arad44.Text
a45 = arad45.Text
a46 = arad46.Text

a51 = arae51.Text
a52 = arae52.Text
a53 = arae53.Text
a54 = arae54.Text
a55 = arae55.Text

Ta = arata.Text
Tb = aratb.Text


'Masukkan Nilai a16

a16 = 200 * Ta

araa16.Caption = a16

'Masukkan Nilai a56

a56 = 200 * Tb

arae56.Caption = a56

'Lakukan Eliminasi Gauss terhadap nilai koefisien T

'Eliminasi Pertama
u1 = a21 / a11
b21 = a21 - (u1 * a11)
b22 = a22 - (u1 * a12)
b23 = a23 - (u1 * a13)
b24 = a24 - (u1 * a14)
b25 = a25 - (u1 * a15)
b26 = a26 - (u1 * a16)

'Eliminasi Kedua
u2 = a31 / a11
c31 = a31 - (u2 * a11)
c32 = a32 - (u2 * a12)
c33 = a33 - (u2 * a13)
c34 = a34 - (u2 * a14)
c35 = a35 - (u2 * a15)
c36 = a36 - (u2 * a16)

'Eliminasi Ketiga
u3 = a41 / a11
d41 = a41 - (u3 * a11)
d42 = a42 - (u3 * a12)
d43 = a43 - (u3 * a13)
d44 = a44 - (u3 * a14)
d45 = a45 - (u3 * a15)
d46 = a46 - (u3 * a16)

'Eliminasi Keempat
u4 = a51 / a11
e51 = a51 - (u4 * a11)
e52 = a52 - (u4 * a12)
e53 = a53 - (u4 * a13)
e54 = a54 - (u4 * a14)
e55 = a55 - (u4 * a15)
e56 = a56 - (u4 * a16)

'Eliminasi Kelima
u5 = c32 / b22
f31 = c31 - (u5 * b21)
f32 = c32 - (u5 * b22)
f33 = c33 - (u5 * b23)
f34 = c34 - (u5 * b24)
f35 = c35 - (u5 * b25)
f36 = c36 - (u5 * b26)

'Eliminasi Keenam
u6 = d42 / b22
g41 = d41 - (u6 * b21)
g42 = d42 - (u6 * b22)
g43 = d43 - (u6 * b23)
g44 = d44 - (u6 * b24)
g45 = d45 - (u6 * b25)
g46 = d46 - (u6 * b26)

'Eliminasi Ketujuh
u7 = e52 / b22
h51 = e51 - (u7 * b21)
h52 = e52 - (u7 * b22)
h53 = e53 - (u7 * b23)
h54 = e54 - (u7 * b24)
h55 = e55 - (u7 * b25)
h56 = e56 - (u7 * b26)

'Eliminasi Kedelapan
u8 = g42 / f33
i41 = g41 - (u8 * f31)
i42 = g42 - (u8 * f32)
i43 = g43 - (u8 * f33)
i44 = g44 - (u8 * f34)
i45 = g45 - (u8 * f35)
i46 = g46 - (u8 * f36)

'Eliminasi Kesembilan
u9 = h53 / f33
j51 = h51 - (u9 * f31)
j52 = h52 - (u9 * f32)
j53 = h53 - (u9 * f33)
j54 = h54 - (u9 * f34)
j55 = h55 - (u9 * f35)
j56 = h56 - (u9 * f36)

'Eliminasi Kesepuluh
u10 = j53 / i44
k51 = j51 - (u10 * i41)
k52 = j52 - (u10 * i42)
k53 = j53 - (u10 * i43)
k54 = j54 - (u10 * i44)
k55 = j55 - (u10 * i45)
k56 = j56 - (u10 * i46)

'Substitusi Balik

T5 = k56 / k55
T4 = (i46 - (i45 * T5)) / i44
T3 = (f36 - ((f35 * T5) + (f34 * T4))) / f33
T2 = (b26 - ((b25 * T5) + (b24 * T4) + (b23 * T3))) / b22
T1 = (a16 - ((a15 * T5) + (a14 * T4) + (a13 * T3) + (a12 * T2))) / a11

'Tampilkan hasil T1, T2, T3, T4, T5
hasilt1.Caption = T1
hasilt2.Caption = T2
hasilt3.Caption = T3
hasilt4.Caption = T4
hasilt5.Caption = T5


End Sub

3. Jalankan program lalu masukkan nilai koefisien di depat nilai T1, T2, T3, T4, T5 dan masukkan nilai Ta dan Tb sehingga berikut hasilnya :

Dari hasil visual basic dapat terlihat distribusi temperatur di sepanjang batang. Semakin menuju ke arah titik A, temperatur semakin menurun dan itu menunjukkan fenomena konduksi terjadi secara alamiah yaitu panas berpindah dari temperatur yang tinggi menuju temperatur yang lebih rendah. Sekarang kita mengetahui bahwa persebaran temperatur adalah sebagai berikut :

Ta = 100 oC
T1 = 109.5 oC
T2 = 128.5 oC
T3 = 147.6 oC
T4 = 166.7 oC
T5 = 333.3 oC
Tb = 500 oC

Dengan menggunakan metode numerik terlihat bahwa permasalahan fisika mampu diselesaikan sehingga kita dapat mengetahui sebaran distribusi temperatur di sepanjang batang.

Mempelajari Sifat-Sifat Dasar Fluida

Depok, 29 Maret 2012

Fluida adalah benda yang dapat mengalir. Segala sesuatu yang mengalir di muka bumi ini termasuk dalam kategori fluida. Ilmu pengetahuan alam sebagai bagian dari seluruh ilmu di dunia ini adalah suatu ilmu yang mejelaskan proses atau fenomena yang terjadi secara alamiah di muka bumi ini. Oleh sebab itu, berdasarkan kata ilmu pebgetahuan alam, maka segala fenomena yang terjadi di alam ini pasti bisa dijelaskan oleh ilmu pengetahuan.

Fluida merupakan objek yang lazim digunakan untuk melakukan penelitian dalam ranah ilmu pengetahuan alam, khususnya fisika. Fluida secara alamiah dapat mengalir dari tekanan yang lebih tinggi menuju tekanan yang lebih rendah. Begitupun temperatur fluida hanya dapat berpindah dari temperatur tinggi menuju temperatur rendah. Energi yang terkandung di dalam fluida pun hanya dapat ditransfer dari potensial yang tinggi menuju potensial yang rendah.

Alam telah memberikan tanda-tanda kepada manusia sebagai penghuninya untuk belajar tentang sifat-sifat dari fluida itu sendiri. Dari fenomena alam yang terjadi di muka bumi ini, maka manusia yang telah dikaruniai kemampuan untuk berpikir mulai berpikir dan mendalami tentang gejala dan fenomena yang terjadi pada alam sekitarnya.

Makhluk-makhluk ciptaan Tuhan juga secara tak langsung mengajarkan kepada manusia bahwasanya dengan mempelajari semua benda yang ada di alam, maka manusia dapat menjalani hidupnya dengan baik. Dari melihat sifat dan perilaku burung yang mampu terbang, manusia akhirnya berpikir untuk menciptakan alam yang mampu terbang seperti burung. Ketika manusia mulai berpikir, maka ditemukanlah rahasia alam bahwasanya sayap burung memanfaatkan perbedaan tekanan dari fluida yang mengalir di atas dan di bawah permukaan sayap burung. Oleh karena itu manusia mencoba untuk menciptakan sayap yang mengadopsi sayap burung, maka lahirlah pesawat terbang.

Kemudian untuk penerangan di bumi, manusia kemudian mempelajari sifat-sifat air. Air hanya dapat mengalir dari potensial yang tinggi menuju potensial yang rendah. Kemudian manusia membendung air dalam jumlah besar atau yang sering kita kenal sebagai bendungan. Bendungan memiliki ketingian yang lebih tinggi dari permukaan tanah, sehingga air memiliki energi potensial yang sangat besar. Dari bendungan tersebut air dialirkan sehingga energi air yang cupuk besar tersebut mampu untuk memutar turbin dan selanjutnya turbin memutar generator sehingga terciptalah aliran listrik.

Sifat aliran yang sering juga digunakan manusia dalam kehidupan sehari-hari adalah pada sistem pemipaan. Dengan adanya pipa, maka air mampu dialirkan dari suatu tempat ke tempat yang lain. Dengan mempelajari sifat aliran dalam ilmu fisika maka manusia telah menjawab fenomena alam di mana selama ini air selalu mengalir dari suatu tempat ke tempat lain melalui sungai walaupun jarak antara 2 tempat tersebut saling berjauhan.

Dengan ilmu pengetahuan alam, maka kita sebagai manusia mampu mempelajari sifat dan fenomena yang terjadi di alam sehingga pada akhirnya kita mampu memanfaatkannya untuk kehidupan kita sebagai umat manusia.

Simulasi Tsunami Dengan Menggunakan CFD

Depok, 28 Maret 2012

Siapa yang tidak kenal dengan tsunami?? Mungkin sebelum kejadian tsunami di Aceh pada Desember  2004 atau bahkan tsunami di Jepang pada Maret 2011 kita hanya menganggap tsunami sebatas dongeng belaka. Namun sejak kejadian di kedua tempat berbeda itu mata kita seolah-olah terbuka bahwasanya kejadian tsunami itu memang dapat mengintai kita dan merupakan kejadian yang nyata terjadi. Namun banyak diantara kita yang tidak mengetahui mengapa sebenarnya tsunami dapat terjadi dan bagaimana ilmu pengetahuan alam mampu menjelaskan fenomena tsunami tersebut.

FENOMENA TSUNAMI

Tsunami terjadi akibat adanya perpatahan lempeng atau pergeseran lempeng bumi sehingga yang pada awalnya permukaan laut relatif tenang, dengan adanya pergeseran lempeng tersebut maka permukaan laut menjadi naik akibat terdapat gangguan.

Dalam bentuk apakah gangguan tersebut?

Gangguan yang diakibatkan oleh perpatahan lempeng bumi berupa energi. Adapun energi yang dihasilkan tersebut berbentuk impuls. Impuls adalah gaya yang terjadi secara tiba-tiba dalam kurun waktu tertentu. Perpatahan lempeng atau pergeseran lempeng bumi terjadi dalam kurun waktu tertentu. Perpatahan atau pergeseran lempeng bumi tersebut menghasilkan gaya yang sangat besar, sehingga gangguan tersebut menghasilkan impuls. Impuls dapat ditulis dengan model matematika sebagai berikut :

Dengan adanya gangguan impuls, maka terjadi perubahan momentum. Perubahan momentum dapat dilihat ketika pada kondisi 1, air laut mengalir dengan tenang, dengan massa dan kecepatan tertentu. Namun ketika terjadi patahan atau pergeseran lempeng, maka kecepatan air akan berubah menjadi lebih cepat. Hal itulah yang menyebabkan tsunami begitu dahsyat. Berikut ilustrasinya :

Impuls merupakan perubahan momentum, sehingga kita dapat menuliskan :

Semakin lamanya waktu terjadinya patahan lempengan maka nilai impuls akan semakin besar, akibatnya dengan semakin besarnya impuls, maka nilai kecepatan kedua ( V2) akan semakin besar, akibatnya gelombang tsunami akan semakin dahsyat.

Begitulah penjelasan mengenai proses terjadinya tsunami yang telah mampu dijelaskan menggunakan pendekatan ilmu pengetahuan alam, khususnya ilmu fisika.

Pemrograman

Pemrograman adalah proses menulis, menguji dan memperbaiki (debug), dan memelihara kode yang membangun sebuah program komputer. Kode ini ditulis dalam berbagai bahasa pemrograman. Tujuan dari pemrograman adalah untuk memuat suatu program yang dapat melakukan suatu perhitungan atau 'pekerjaan' sesuai dengan keinginan si pemrogram. Untuk dapat melakukan pemrograman, diperlukan keterampilan dalam algoritma, logika, bahasa pemrograman, dan di banyak kasus, pengetahuan-pengetahuan lain seperti matematika.
Pemrograman adalah sebuah seni dalam menggunakan satu atau lebih algoritma yang saling berhubungan dengan menggunakan sebuah bahasa pemrograman tertentu sehingga menjadi sebuah program komputer. Bahasa pemrograman yang berbeda mendukung gaya pemrograman yang berbeda pula. Gaya pemrograman ini biasa disebut paradigma pemrograman.
Apakah memprogram perangkat lunak lebih merupakan seni, ilmu, atau teknik telah lama diperdebatkan. Pemrogram yang baik biasanya mengkombinasikan tiga hal tersebut, agar dapat menciptakan program yang efisien, baik dari sisi waktu berjalan (running time), atau memori.

Untuk melakukan pemrograman, maka kita harus memakai bahasa pemrograman. Bahasa pemrograman harus menggunakan bahasa komputer agar komputer mampu memahami deretan algoritma yang telah kita buat. Bahasa pemrograman, atau sering diistilahkan juga dengan bahasa komputer, adalah teknik komando/instruksi standar untuk memerintah komputer. Bahasa pemrograman ini merupakan suatu himpunan dari aturan sintaks dan semantik yang dipakai untuk mendefinisikan program komputer. Bahasa ini memungkinkan seorang programmer dapat menentukan secara persis data mana yang akan diolah oleh komputer, bagaimana data ini akan disimpan/diteruskan, dan jenis langkah apa secara persis yang akan diambil dalam berbagai situasi.

Menurut tingkat kedekatannya dengan mesin komputer, bahasa pemrograman terdiri dari:

1. Bahasa Mesin, yaitu memberikan perintah kepada komputer dengan memakai kode bahasa biner, contohnya 01100101100110
2. Bahasa Tingkat Rendah, atau dikenal dengan istilah bahasa rakitan (bahasa Inggris Assembly), yaitu memberikan perintah kepada komputer dengan memakai kode-kode singkat (kode mnemonic), contohnya MOV, SUB, CMP, JMP, JGE, JL, LOOP, dsb.
3. Bahasa Tingkat Menengah, yaitu bahasa komputer yang memakai campuran instruksi dalam kata-kata bahasa manusia (lihat contoh Bahasa Tingkat Tinggi di bawah) dan instruksi yang bersifat simbolik, contohnya {, }, ?, <<, >>, &&, ||, dsb.
4. Bahasa Tingkat Tinggi, yaitu bahasa komputer yang memakai instruksi berasal dari unsur kata-kata bahasa manusia, contohnya begin, end, if, for, while, and, or, dsb.

Sebagian besar bahasa pemrograman digolongkan sebagai Bahasa Tingkat Tinggi, hanya bahasa C yang digolongkan sebagai Bahasa Tingkat Menengah dan Assembly yang merupakan Bahasa Tingkat Rendah.

Perbedaan bahasa pemrograman dapat menjadi penyebab perbedaan paradigma pemrograman. Pilihan bahasa pemrograman dipengaruhi banyak alasan, seperti kecocokan dengan kriteria program dan jenis aplikasi yang akan dibuat.

Beberapa bahasa pemrograman adalah:

• Pascal
• Basic
• C atau C++
• Cobol
• Java
• Fortran
• Ada
• Clipper

Dengan adanya bahasa pemrograman seperti yang telah disebutkan diatas, maka algoritma yang merupakan bahasa manusia (hasil pola pikir manusia) diubah atau diterjemahkan ke dalam bahasa pemrograman komputer sehingga komputer dapat memahami urutan prosedur yang telah kita buat. Hal ini dikarenakan cara berpikir komputer lebih rumit dan berbeda dengan otak manusia. Oleh karena itu pemrograman menggunakan bahasa pemrograman menjadi hal yang sangat penting.

Algoritma

Algoritma adalah suatu proses atau urutan langkah dari suatu proses. Dalam matematika dan komputasi, algoritma atau algoritme merupakan kumpulan perintah untuk menyelesaikan suatu masalah. Perintah-perintah ini dapat diterjemahkan secara bertahap dari awal hingga akhir. Masalah tersebut dapat berupa apa saja, dengan catatan untuk setiap masalah, ada kriteria kondisi awal yang harus dipenuhi sebelum menjalankan algoritma. Algoritma akan dapat selalu berakhir untuk semua kondisi awal yang memenuhi kriteria, dalam hal ini berbeda dengan heuristik. Algoritma sering mempunyai langkah pengulangan (iterasi) atau memerlukan keputusan (logika Boolean dan perbandingan) sampai tugasnya selesai.

Desain dan analisis algoritma adalah suatu cabang khusus dalam ilmu komputer yang mempelajari karakteristik dan performa dari suatu algoritma dalam menyelesaikan masalah, terlepas dari implementasi algoritma tersebut. Dalam cabang disiplin ini algoritma dipelajari secara abstrak, terlepas dari sistem komputer atau bahasa pemrograman yang digunakan. Algoritma yang berbeda dapat diterapkan pada suatu masalah dengan kriteria yang sama.

Kompleksitas dari suatu algoritma merupakan ukuran seberapa banyak komputasi yang dibutuhkan algoritma tersebut untuk menyelesaikan masalah. Secara informal, algoritma yang dapat menyelesaikan suatu permasalahan dalam waktu yang singkat memiliki kompleksitas yang rendah, sementara algoritma yang membutuhkan waktu lama untuk menyelesaikan masalahnya mempunyai kompleksitas yang tinggi.

Sejarah Algoritma


Kata algoritma berasal dari latinisasi nama seorang ahli matematika dari Uzbekistan Al Khawārizmi (hidup sekitar abad ke-9), sebagaimana tercantum pada terjemahan karyanya dalam bahasa latin dari abad ke-12 "Algorithmi de numero Indorum". Pada awalnya kata algorisma adalah istilah yang merujuk kepada aturan-aturan aritmetis untuk menyelesaikan persoalan dengan menggunakan bilangan numerik arab (sebenarnya dari India, seperti tertulis pada judul di atas). Pada abad ke-18, istilah ini berkembang menjadi algoritma, yang mencakup semua prosedur atau urutan langkah yang jelas dan diperlukan untuk menyelesaikan suatu permasalahan. Masalah timbul pada saat akan menuangkan bagaimana proses yang harus dilalui dalam suatu/sebuah sistem (program) bagi komputer sehingga pada saat eksekusinya, komputer dapat bekerja seperti yang diharapkan. Programer komputer akan lebih nyaman menuangkan prosedur komputasinya atau urutan langkah proses dengan terlebih dahulu membuat gambaran (diagram alur) diatas kertas.

Jenis-jenis algoritma

Terdapat beragam klasifikasi algoritma dan setiap klasifikasi mempunyai alasan tersendiri. Salah satu cara untuk melakukan klasifikasi jenis-jenis algoritma adalah dengan memperhatikan paradigma dan metode yang digunakan untuk mendesain algoritma tersebut. Beberapa paradigma yang digunakan dalam menyusun suatu algoritma akan dipaparkan dibagian ini. Masing-masing paradigma dapat digunakan dalam banyak algoritma yang berbeda.

• Divide and Conquer, paradigma untuk membagi suatu permasalahan besar menjadi permasalahan-permasalahan yang lebih kecil. Pembagian masalah ini dilakukan terus menerus sampai ditemukan bagian masalah kecil yang mudah untuk dipecahkan. Singkatnya menyelesaikan keseluruhan masalah dengan membagi masalah besar dan kemudian memecahkan permasalahan-permasalahan kecil yang terbentuk.

• Dynamic programming, paradigma pemrograman dinamik akan sesuai jika digunakan pada suatu masalah yang mengandung sub-struktur yang optimal dan mengandung beberapa bagian permasalahan yang tumpang tindih. Paradigma ini sekilas terlihat mirip dengan paradigma Divide and Conquer, sama-sama mencoba untuk membagi permasalahan menjadi sub permasalahan yang lebih kecil, tapi secara intrinsik ada perbedaan dari karakter permasalahan yang dihadapi.

 Berikut akan ditampilkan contoh diagram algoritma sederhana :

Dari diagram di atas dapat dijelaskan bahwa terdapat prosedur untuk melakukan pengujian apakah lampu rusak atau tidak. Kita harus memasang lampu dan mengaliri lampu dengan arus listrik dengan cara menyalakan saklar. Kemudian kita amati, apabila lampu nyala, maka lampu dalam keadaan normal, namun apabila lampu tidak menyala, maka lampu rusak. Langkah berikutnya apabila kita telah mengetahui lampu tersebut rusak adalah dengan mengganti bohlam dan kemudian proses selesai.

Aliran Fluida Diantara 2 Plat Sejajar

Depok, 28 Maret 2012

Ketika suatu fluida mengalir pada sebuah pipa, maka dianggap bahwa fluida mengalir pada dua plat sejajar. Kita dapat melihat bagaimana fenomena kecepatan fluida tersebut ketika mengalir diantara dua plat sejajar tersebut. Distribusi kecepatan aliran fluida ternyata tidaklah sama. Untuk melihat fenomena aliran fluida tersebut,maka berikut akan dilakukan simulasi CFD pada kasus berikut :

Dari gambar di atas, terdapat dua plat yang sejajar dengan jarak H=0,2 m  dan dengan panjang L=1m, lalu dialirkan udara (laminar) dengan densitas r=1,2 kg/m³.

Terdapat 2 Kasus yang terdapat dalam contoh ini

Yaitu dengan mengganti salah satu parameter

1.       Mengganti viskositas m=4x10^-5 kg/m.s dan m= 10^-5 kg/m.s dengan menetapkan kecepatan inlet u_inlet=0,01m/s

2.       Mengganti kecepatan inlet u_inlet=0,01m/s dan u_inlet=0,04m/s dengan menetapkan viskositas m=4x10^-5 kg/m.s

Marilah kita buat langkah-langkah untuk membuat simulasi CFD

Ukuran Cell  50 x 10

Kasus 1 dengan viskositas 4x10^-5 kg/m.s dan inlet u_inlet=0,01m/s

1.       Kita buat atur domain untuk membuat ukuran, yaitu panjang  1 m dan tinggi 0.2 m. Terlebih dahulu dibuatkan cell dengan ukuran yang agak renggang yaitu 50 cell untuk panjang dan 10 cell untuk tinggi. Adapun pengaturan cell dapat diatur pada jumlah cell. Setelah itu kita atus sempadan di mana sisi paling kiri dijadikan inlet, sisi kanan dijadikan outlet, sisi atas-bawah dijadikan wall dan bagian tengan dijadikan live. Hasilnya adalah sebagai berikut :

2.       Atur kf dengan memasukkan densitas 1.2  kg/m³ dan viskositas 4 x 10^-5 kg/m.s dan kecepatan u sebesar 0.01 m/s . Setelah itu atur ks untuk memasukkan nilai kecepatan u  = 0.01 m/s

3.       Kemudian lakukan iterasi dan tampilkan hasilnya sebagai berikut :

Kasus 1 dengan m=1x10^-5 kg/m.s dan inlet u_inlet=0,01m/s

Untuk memulai kasus 1 dengan perubahan nilai viskositas menjadi 1x10^-5 kg/m.s maka kita tinggal ketik kf dan pada viskositas ubah viskositas menjadi 1x10^-5 kg/m.s. Kemudian lakukan iterasi kembali dan tampilkan hasilnya sebagai berikut :

Kasus 2 dengan viskositas 4x10^-5 kg/m.s dan inlet u_inlet=0,01m/s hasilnya sama dengan Kasus 1 dengan  viskositas 4x10^-5 kg/m.s dan inlet u_inlet=0,01m/s

Kasus 2 dengan viskositas 4x10^-5 kg/m.s dan inlet u_inlet=0,04m/s

Untuk memulai kasus 2 dengan perubahan nilai viskositas menjadi 4x10^-5 kg/m.s dan kecepatan u  = 0.01 m/s maka kita tinggal ketik kf dan pada viskositas ubah viskositas menjadi 4x10^-5 kg/m.s lalu pada ks ubah kecepatan u menjadi 0.04 m/s . Kemudian lakukan iterasi kembali dan tampilkan hasilnya sebagai berikut :

Ukuran Cell 200 x 20

 Kasus 1 dengan viskositas 4x10^-5 kg/m.s dan inlet u_inlet=0,01m/s

Setelah melakukan simulasi dengan ukuran cell 50 x 10, maka selanjutkan akan dilakukan pemadatan cell menjadi 200 x 20 cell. Hal ini dilakukan agar hasil simulasi semakin bagus karena grid menjadi lebih rapat. Adapun langkah-langkah sama seperti langkah sebelumnya hanya saja jumlah cell diubah menjadi panjang 200 cell dan tinggi 20 cell.

2.       Atur kf dengan memasukkan densitas 1.2  kg/m³ dan viskositas 4 x 10^-5 kg/m.s dan kecepatan u sebesar 0.01 m/s . Setelah itu atur ks untuk memasukkan nilai kecepatan u  = 0.01 m/s

3.       Kemudian lakukan iterasi dan tampilkan hasilnya sebagai berikut :

Kasus 1 dengan m=1x10^-5 kg/m.s dan inlet u_inlet=0,01m/s

Untuk memulai kasus 1 dengan perubahan nilai viskositas menjadi 1x10^-5 kg/m.s maka kita tinggal ketik kf dan pada viskositas ubah viskositas menjadi 1x10^-5 kg/m.s. Kemudian lakukan iterasi kembali dan tampilkan hasilnya sebagai berikut :

  

Kasus 2 dengan viskositas 4x10^-5 kg/m.s dan inlet u_inlet=0,01m/s hasilnya sama dengan Kasus 1 dengan viskositas 4x10^-5 kg/m.s dan inlet u_inlet=0,01m/s

Kasus 2 dengan viskositas 4x10^-5 kg/m.s dan inlet u_inlet=0,04m/s

Untuk memulai kasus 2 dengan perubahan nilai viskositas menjadi 4x10^-5 kg/m.s dan kecepatan u  = 0.01 m/s maka kita tinggal ketik kf dan pada viskositas ubah viskositas menjadi 4x10^-5 kg/m.s lalu pada ks ubah kecepatan u menjadi 0.04 m/s . Kemudian lakukan iterasi kembali dan tampilkan hasilnya sebagai barikut :

Apabila dilihat maka hasilnya adalah sebagai berikut :

 Data di atas dapat dijelaskan menggunakan pendekatan Reynold Number yaitu :

Apabila kita analisa dapat kita lihat bahwa ketika kecepatan konstan dan viskositas bervariasi, maka semakin besar viskositas, maka dari rumus Reynold Number terlihat bahwa nilai Reynold Number semakin kecil seiring dengan bertambahnya viskositas, hal itu menyebabkan aliran semakin laminar. Semakin laminar maka akiran semakin tenang sehingga lebih cepat membentuk Fully Develped Region . Hal itu dapat dilihat dengan semakin pendeknya zona dari Entrance Region . Hal sebaliknya ketika viskositas semakin rendah, maka Reynold Number semakin besar, akibatnya aliran semakin turbulen dan aliran semakin acak akibatnya aliran semakin lama untuk mencapai Fully Develped Region . Hal itu dapat dilihat dengan semakin panjangnya  zona dari Entrance Region .

Ketika  Viskositas konstan, maka semakin besar kecepatan, maka Reynold Number semakin besar, akibatnya aliran semakin turbulen dan aliran semakin acak akibatnya aliran semakin lama untuk mencapai Fully Develped Region . Hal itu dapat dilihat dengan semakin panjangnya  zona dari Entrance Region . Hal sebaliknya ketika kecepatan semakin kecil, maka semakin besar viskositas, maka dari rumus Reynold Number terlihat bahwa nilai Reynold Number semakin kecil seiring dengan bertambahnya viskositas, hal itu menyebabkan aliran semakin laminar. Semakin laminar maka akiran semakin tenang sehingga lebih cepat membentuk Fully Develped Region . Hal itu dapat dilihat dengan semakin pendeknya zona dari Entrance Region .

Adapun perbedaan dari jumlah cell mempengaruhi kerapatan dari kontur, semakin sedikit jumlah cell maka kontur semakin renggang. Sebaliknya ketika jumlah cell diperbanyak maka kontur semakin rapat sehingga gambar semakin jelas. Semakin jelas gambar kontur, maka fenomena fisika dari aliran lebih mudah untuk diamati dan dianalisa. 

Metode Iterative Bisection

Depok, 28 Maret 2012

Setelah membahas mengenai teori metode iterative, maka pada postingan kali ini akan dijelaskan mengenai aplikasi dari metode iterative tersebut. metode yang dipilih pada contoh aplikasi ini adalah metode bisection. Berikut akan dijelaskan sedikit tentang metode bisection.

Metode Bidang Bebas atau lebih spesifik lagi ‘Metode Bidang Paruh’ (Bisection) adalah “pemaruhan”(nilai rata-rata) dari nilai estimasi akar suatu persamaan aljabar non-linear tunggal yang dibentuk dengan cara menebak 2 buah harga awal pada interval [a,b] yang bertempat-kedudukan ‘mengapit’ (di kiri dan kanan) akar atau jawab yang sebenarnya. Metode ini pada umumnya memerlukan 2 (dua) buah tebakan untuk harga-harga x-awal (x0 dan x1).

Untuk contoh aplikasi metode bisection menggunakan contoh 3.1 buku rajaraman halaman 38 dengan persamaan :

X² – d = f (x) = 0

dimana nilai tebakan awal d = 25.0 ; x0 = 2.0 ; dan x1 = 7.0

Dengan metode bisection ini kita akan mencari akar-akar dari persamaan di atas.

Berikut adalah langkah-langkah untuk menjalankan metode bisection :

1. Buat userform dan buatlah kotak-kotak sesuai kebutuhan sesuai gambar di bawah ini :

2. Buat variabel dan rumus untuk metode bisection, yaitu nilai X2, f (X0), f(X1), f(X2), iterasi X2, iterasi f(X0), iterasi f(X1) dan iterasi f(X2)

3. Buatlah program seperti dibawah ini pada commandbutton :

Private Sub CommandButton1_Click()

'Program ini adalah program metode iterative bisection

'Komputasi Teknik

'Arandityo Narutomo 1106107782

'METODE BISECTION

'Persamaan dari program ini adalah X^2-d = f(x) = 0

'Definisi variabel

'y0=F(x0)

'y1=F(x1)

'y2=F(x2)

Dim x0, x1, x2, y0, y1, y2, n, e, d As Double

x0 = Int(TextBox1.Text)

x1 = Int(TextBox2.Text)

n = Int(TextBox7.Text)

d = 25

'Rumus perhitungan bisection

x2 = (x0 + x1) / 2

TextBox3.Text = x2

y0 = x0 ^ 2 - d

TextBox4.Text = y0

y1 = x1 ^ 2 - d

TextBox5.Text = y1

y2 = x2 ^ 2 - d

TextBox6.Text = y2

'Perhitungan Error

e = ((x2 - x1) / x2) * 100

If e < 0 Then e = e * -1

TextBox8.Text = e

'Persamaan iterasi f(x)=X^2-d

For i = 0 To n

      x2 = (x0 + x1) / 2

  If (x0 ^ 2 - d) * (x2 ^ 2 - d) <= 0 Then

      x1 = x2

  Else

      x0 = x2

  End If

  ListBox1.AddItem x2

'Listbox F (x0)

y0 = x0 ^ 2 - d

'Listbox F (x1)

y1 = x1 ^ 2 - d

'Listbox F (x2)

y2 = x2 ^ 2 - d

ListBox2.AddItem y0

ListBox3.AddItem y1

ListBox4.AddItem y2

'Iterasi error

e = ((x2 - x1) / x2) * 100

If (((x2 - x1) / x2) * 100) < 0 Then e = e * -1

ListBox5.AddItem e

Next i

End Sub

4. Tampilkan hasilnya sebagai berikut

Masukkan Input 

Maka hasilnya seperti di bawah ini

Dari data di atas, kita ketahui bahwa nilai X2 berkisar 5. Dengan melihat bahwa error sudah mendekati nol atau bahkan nol, nilai X2 tetap ada dikisaran 5. Karena persamaan yang ingin dicari akar-akarnya mengindikasikan bahwa akar kembar, maka nilai X0 dan X1 adalah sama, sehingga dari data X2 yang telah diketahui sekitar 5, maka

Jumlah X0 dan X1 = 2 x 5 = 10, sehingga nilai X0 dan X1 adalah 1/2 x 10 = 5.

Apabila dilihat dari buku Rajaraman hasilnya sebagai berikut :

Dari nilai di atas terlihat baik hasil X0 dan X1 hampir serupa yaitu sekitar 5. Hal ini menunjukkan bahwa metode iterative bisection yang telah dibuat pada visual basic hampir sama dengan versi buku Rajaraman

Aplikasi Integrasi Numerik Metode Trapezoida dan Metode Simphson

Depok, 27 Maret 2012

Setelah diposting mengenai teori dari integrasi numerik, maka sekarang akan dibahas mengenai perbedaan antara metode trapezoida dan metode simphson. Berikut sedikit dijelaskan perbedaan metode trapezoida dan metode simphson.

• Aturan Trapezoidal

• Aturan Simpson

Berikut adalah langkah-langkah pembuatan program integrasi numerik :

1. Buat userform terlebih dahulu kemudian isi kotak-kotak sesuai dengan kebutuhan sesuai dengan gambar di bawah :

 

2. Definisikan setiap kotak-kotak agar memberikan hasil yang sesuai

3. Definisikan nilai X dan f (x)

4. Buat Rumus metode trapezoida dan metode simphson

5. Buatlah program seperti dibawah ini

Private Sub CommandButton1_Click()

'Ini adalah program untuk melakukan integrasi secara numerik

'Program ini mencoba membandingkan metode trapezoida dan simphson

'Arandityo Narutomo 1106107782

'Komputasi Teknik

Dim x1, x2, x3, x4, x5, x6, x7, x8, x9, x10 As Double

Dim y1, y2, y3, y4, y5, y6, y7, y8, y9, y10 As Double

Dim h, Hasil_Trapezoida, Hasil_Simphson As Double

'Definiskan variabel-variabel x dan y = f (x)

x1 = arax1.Text

x2 = arax2.Text

x3 = arax3.Text

x4 = arax4.Text

x5 = arax5.Text

x6 = arax6.Text

x7 = arax7.Text

x8 = arax8.Text

x9 = arax9.Text

x10 = arax10.Text

y1 = arafo1.Text

y2 = arafo2.Text

y3 = arafo3.Text

y4 = arafo4.Text

y5 = arafo5.Text

y6 = arafo6.Text

y7 = arafo7.Text

y8 = arafo8.Text

y9 = arafo9.Text

y10 = arafo10.Text

'Definikan nilai h

h = x2 - x1

Hasil_Trapezoida = h / 2 * (y1 + (2 * y2) + (2 * y3) + (2 * y4) + (2 * y5) + (2 * y6) + (2 * y7) + (2 * y8) + (2 * y9) + y10)

Hasil_Simphson = h / 3 * (y1 + (4 * y2) + (2 * y3) + (4 * y4) + (2 * y5) + (4 * y6) + (2 * y7) + (4 * y8) + (2 * y9) + y10)

Hasilh.Caption = h

HasilTrapezoida.Caption = Hasil_Trapezoida

HasilSimphson.Caption = Hasil_Simphson

End Sub

6. Tampilkan hasil program sebagai berikut :

Dari hasil diatas baik menggunakan metode trapezoida maupun metode simphson menghasilkan hasil perhitungan yang hampir sama, namun metode trapezoida menghasilkan luasan yang lebih besar dibandingkan dengan metode simphson. Namun pada dasarnya baik metode trapezoida maupun metode simphson sama-sama menghasilkan hasil yang hampir sama.

Teori Penyelesaian Persamaan Aljabar Simultan

Depok, 27 Maret 2012

Penyelesaian persamaan aljabar simultan merupakan suatu metode untuk mendapatkan himpunan penyelesaian dari beberapa persamaan aljabar linear. Ketika jumlah persamaan berjumlah 2 buah dan variabel yang dicari berjumlah 2 buah, mungkin kita masih bisa menyelesaikan dengan sederhana, namun apabila jumlah persamaan sudah berjumlah cukup banyak dan variable yang harus dicari juga semakin banyak, maka kita akan menemui kesulitan untuk menyelesaikannya secara manual. Untuk itu kita membutuhkan bantuan komputer untuk menyelesaikannya. 

Penyelesaian persamaan aljabar simultan biasanya menggunakan metode eliminasi gauss. Eliminasi gauss adalah suatu metode untuk mengilangkan koefisien menggunakan matriks. Berikut adalah contoh dari penerapan eliminasi gauss :

Misalkan terdapat 3 buah persamaan linear sebagai berikut 

a₁₁ x₁  + a₁₂ x₂ + a₁₃ x₃ = a₁₄

a₂₁ x₁ +  a₂₂ x₂ + a₂₃ x₃ = a₂₄

a₃₁ x₁ +  a₃₂ x₂ + a₃₃ x₃ = a₃₄

Himpunan penyelesaian dari 3 buah persamaan linear di atas adalah mendapatkan nilai x₁ , x₂ , dan x₃ . Untuk mendapatkan himpunan penyelesaian tersebut, maka digunakan metode eliminasi gauss sebagai berikut :

Kita harus terlebih dahulu menuliskan dalam bentuk matriks

                     

Dari matriks di atas, penyelesaian menggunakan metode eliminasi gauss harus membentuk matriks seperti ini
 

                      

Agar matriks berubah menjadi seperti di atas, maka berikut langkah-langkahnya :

‘Eliminasi pertama

Tentukan nilai U₁ = a₂₁ / a₁₁ , sehingga

b₂₁ = a₂₁ – (U₁ . a₁₁)

b₂₂ = a₂₂ – (U₁ . a₁₂)

b₂₃ = a₂₃ – (U₁ . a₁₃)

b₂₄ = a₂₄ – (U₁ . a₁₄)

‘Eliminasi kedua

Tentukan U₂ = a₃₁ / a₁₁

c₃₁ =  a₃₁ – (U₂ . a₁₁)

c₃₂ = a₃₂ – (U₂ . a₁₂)

c₃₃ = a₃₃ – (U₂ . a₁₃)

c₃₄ = a₃₄ – (U₂ . a₁₄)

Setelah eliminasi pertama dan kedua maka susunan persamaan linear menjadi

a₁₁ x₁  + a₁₂ x₂ + a₁₃ x₃ = a₁₄

b₂₁ x₁ +  b₂₂ x₂ + b₂₃ x₃ = b₂₄

c₃₁ x₁ +  c₃₂ x₂ + c₃₃ x₃ = c₃₄

dimana nilai b₂₁ dan c₃₁ adalah nol, tapi nilai c₃₂ masih belum nol sehingga untuk membuat nilai c₃₂ adalah nol, dibutuhkan eliminasi ketiga sebagai berikut :

Tentukan U₃ = c₃₂ / b₂₂

d₃₁ = c₃₁ – ( U₃ . b₂₁ )

d₃₂ = c₃₂ – (U₃ . b₂₂)

d₃₃ = c₃₃ – (U₃ . b₂₃)

d₃₄ = c₃₄ – (U₃ . b₂₄)

Sehingga persamaan sekarang telah menjadi 

a₁₁ x₁  + a₁₂ x₂ + a₁₃ x₃ = a₁₄

b₂₁ x₁ +  b₂₂ x₂ + b₂₃ x₃ = b₂₄

d₃₁ x₁ +  d₃₂ x₂ + d₃₃ x₃ = d₃₄

sehingga matriksnya sekarang menjadi 

                      

Untuk mendapatkan nilai x₁ , x₂ , dan x₃ maka dibutuhkan substitusi balik sebagai berikut :

x₃ = d₃₄ / d₃₃

x₂ = ( b₂₄  - x₃ . b₂₃ ) / b₂₂

x₁ = ( a₁₄ – a₁₃. x₃ – a₁₂ . x₂ ) / a₁₁

Sehingga nilai x₁ x₂ x₃ dapat diketahui.